Approximation Methods for Large Dynamic Stochastic Games
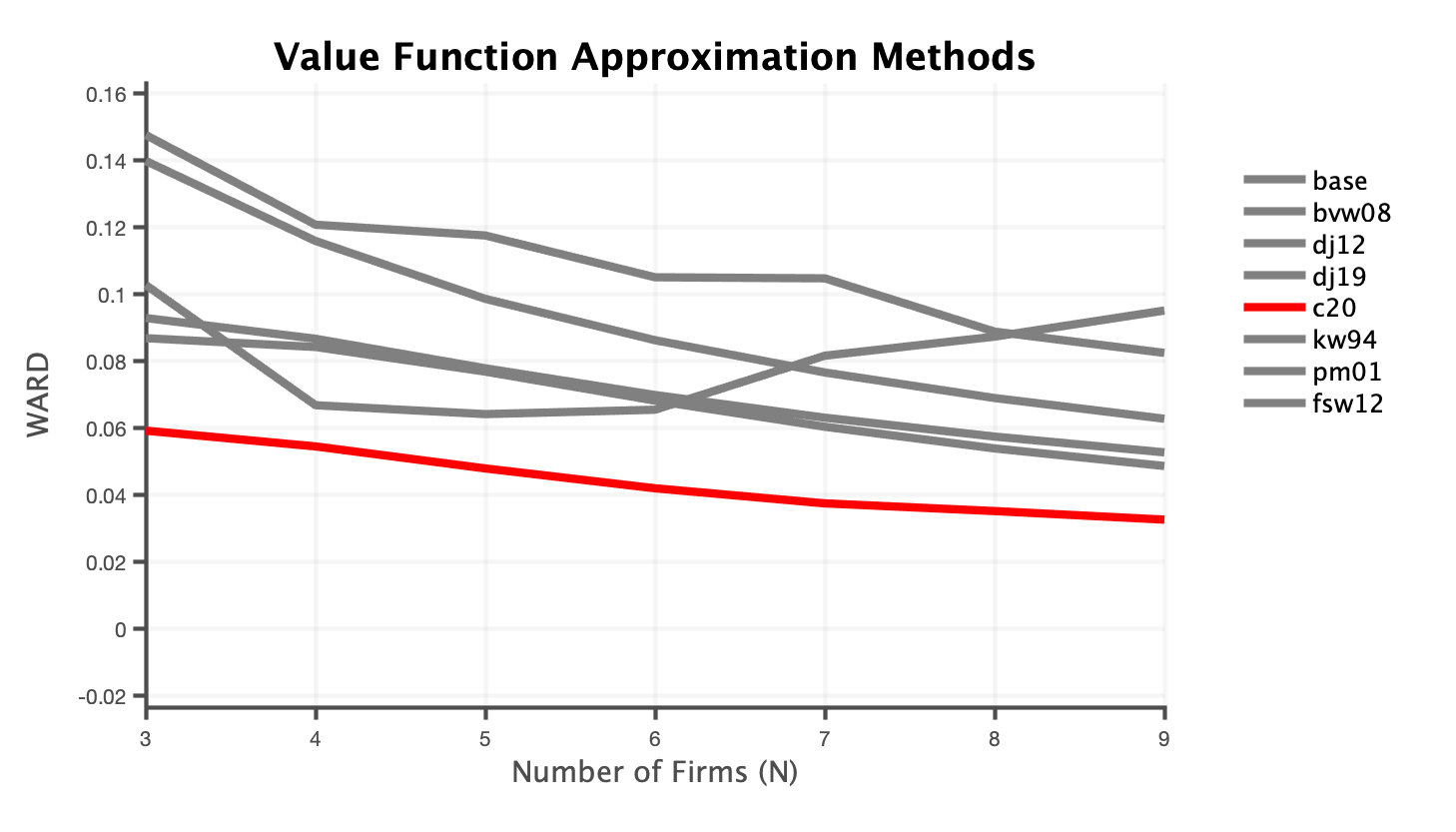 Comparison of existing value function approximation methods (lower is better)
Comparison of existing value function approximation methods (lower is better)
Dynamic stochastic games notoriously suffer from a curse of dimensionality that makes computing the Markov Perfect Equilibrium of large games infeasible. This article compares the existing approximation methods and alternative equilibrium concepts that have been proposed in the literature to overcome this problem. No method clearly dominates the others but some are dominated in all dimensions. In general, alternative equilibrium concepts outperform sampling-based approximation methods. I propose a new game structure, games with random order, in which players move sequentially and the order of play is unknown. The Markov Perfect equilibrium of this game consistently outperforms all existing approximation methods in terms of approximation accuracy while still being extremely efficient in terms of computational time.